| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 10.1 | Exercise 10.2 | Exercise 10.3 |
Chapter 10 Visualising Solid Shapes
Welcome to the solutions guide for Chapter 10: Visualising Solid Shapes. This chapter significantly enhances your journey into the realm of three-dimensional geometry, building upon the introductory concepts from Class 7. The ability to visualize objects in three dimensions (3D) and understand their representation in two dimensions (2D) is a critical aspect of spatial reasoning. This skill is fundamental not only in mathematics but also in numerous fields such as engineering, architecture, design, computer graphics, medicine, and even everyday activities like navigation or assembling objects. This chapter aims to further develop your capacity to mentally perceive, interpret, and represent the shapes that occupy the space around us.
The solutions provided here guide you through key concepts and techniques for better understanding and depicting solid shapes. The journey begins by reinforcing the distinction between 2D (plane) figures, which have only length and width (like squares, circles), and 3D (solid) shapes, which possess length, width, and depth/height (like cubes, spheres). You'll become more familiar with identifying common 3D shapes, including:
- Cubes
- Cuboids
- Cylinders
- Cones
- Spheres
- Pyramids (various types like square-based or triangular-based)
- Prisms (various types like triangular prism)
A primary focus is on understanding how 3D objects can be viewed and represented from different perspectives. The solutions meticulously explain and provide practice in identifying or drawing the principal views of a solid object, often referred to as orthographic projections:
- Top View: What the object looks like when viewed directly from above.
- Front View: What the object looks like when viewed directly from the front.
- Side View: What the object looks like when viewed directly from the side (usually specified as left or right).
Mastering the ability to visualize and sketch these views for various solids, including complex arrangements like stacked cubes, is crucial for interpreting technical drawings and understanding spatial relationships.
The chapter also briefly touches upon the idea of mapping space, introducing elementary concepts related to scale and the relative positioning of objects in a simplified map context, further grounding spatial awareness in practical application.
A significant portion of the chapter, heavily emphasized in the solutions, is dedicated to Polyhedrons. These are specific types of solid shapes characterized by having:
- Flat polygonal Faces (F)
- Straight Edges (E) where the faces meet
- Sharp corners or Vertices (V) where the edges meet
Solutions guide you in identifying and counting F, V, and E for various polyhedrons, including common examples like prisms (which have two identical parallel bases and rectangular side faces) and pyramids (which have a polygonal base and triangular faces meeting at a common apex). The highlight of this section is the exploration and application of Euler's Formula, a remarkable relationship discovered by Leonhard Euler that connects the number of faces, vertices, and edges for any simple, convex polyhedron:
$\mathbf{F + V - E = 2}$
The solutions provide numerous examples where you'll count F, V, and E for given shapes (like cubes, tetrahedrons, prisms) and verify that this formula consistently holds true. Conversely, problems might require you to use Euler's formula to find the number of faces, vertices, or edges if the other two quantities are known. Accompanied by clear diagrams and often organized tables, these exercises are designed to solidify your understanding of the structural properties of polyhedrons and enhance your overall ability to visualize and reason about solid shapes.
Exercise 10.1
Question 1. For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

Answer:
To match each solid object with its corresponding side view and top view, we need to visualize how each object would look from these different perspectives.
1. A bottle (a): The side view is its characteristic bottle shape (iii). The top view is the circular opening of the bottle, which appears as a circle (iv).
2. A weight (b): The side view of the hexagonal weight is a rectangle (i). The top view shows its hexagonal shape with the '5KG' marking (v).
3. A flask (c): The side view is its tall, cylindrical shape with a cap (iv). The top view shows the circular cap and the strap attached to it (ii).
4. Cup and Saucer (d): The side view shows the profile of a cup sitting on a saucer (v). The top view shows the circular cup inside the larger circular saucer, with the cup's handle visible (iii).
5. A container (e): The side view of the square container is a rectangle with a cap on top (ii). The top view is a square with a circular cap in the center (i).
The correct matching is presented in the table below:
| Object | Side View | Top View |
| (a) A bottle | (iii) | (iv) |
| (b) A weight | (i) | (v) |
| (c) A flask | (iv) | (ii) |
| (d) Cup and Saucer | (v) | (iii) |
| (e) A container | (ii) | (i) |
Question 2. For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.
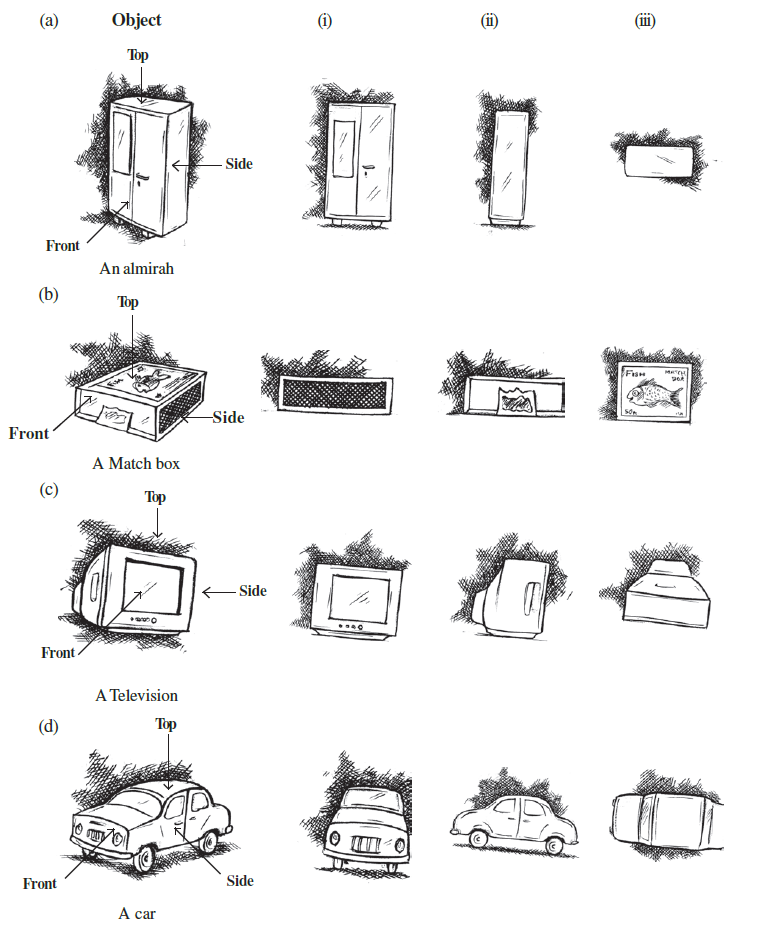
Answer:
To identify the top, front, and side views for each object, we need to observe the object from each of these perspectives as indicated by the arrows in the diagrams.
(a) An almirah
The three views given are (i), (ii), and (iii).
- The Front view shows the doors of the almirah, one with a mirror. This corresponds to view (i).
- The Side view shows the narrow width of the almirah as a plain rectangle. This corresponds to view (ii).
- The Top view shows the rectangular top surface of the almirah. This corresponds to view (iii).
Answer for (a): (i) Front, (ii) Side, (iii) Top
(b) A Match box
The three views given are (i), (ii), and (iii).
- The Front view is the end from which the inner box slides out. This corresponds to view (ii).
- The Side view shows the longer side with the striking surface. This corresponds to view (i).
- The Top view shows the top label of the matchbox, which has a picture of a fish. This corresponds to view (iii).
Answer for (b): (i) Side, (ii) Front, (iii) Top
(c) A Television
The three views given are (i), (ii), and (iii).
- The Front view shows the screen and the control panel. This corresponds to view (i).
- The Side view shows the profile of the television, thicker at the back. This corresponds to view (ii).
- The Top view shows the shape of the television from above. This corresponds to view (iii).
Answer for (c): (i) Front, (ii) Side, (iii) Top
(d) A car
The three views given are (i), (ii), and (iii).
- The Front view shows the front of the car, including the grille and headlights. This corresponds to view (i).
- The Side view shows the profile of the car, including the doors and wheels. This corresponds to view (ii).
- The Top view shows the car from above, including the roof, bonnet, and boot. This corresponds to view (iii).
Answer for (d): (i) Front, (ii) Side, (iii) Top
Question 3. For each given solid, identify the top view, front view and side view.
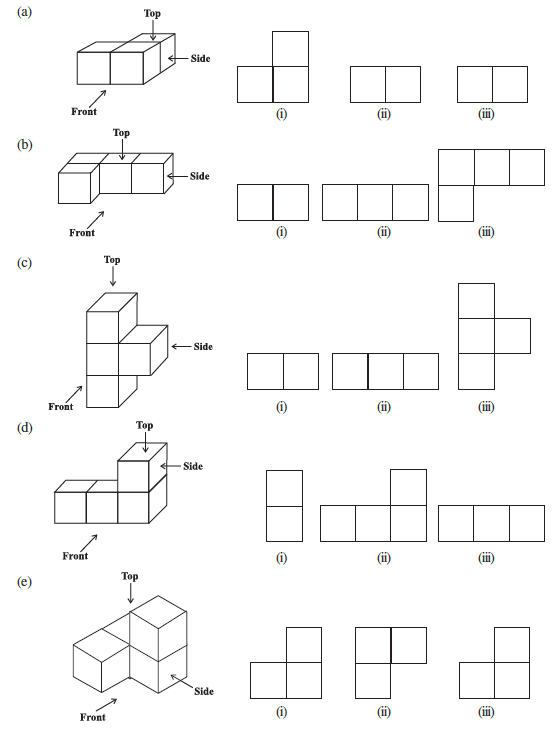
Answer:
(a)
Front View: (ii)
Side View: (iii)
Top View: (i)
(b)
Front View: (ii)
Side View: (i)
Top View: (iii)
(c)
Front View: (iii)
Side View: (ii)
Top View: (i)
(d)
Front View: (ii)
Side View: (i)
Top View: (iii)
(e)
Front View: (i)
Side View: (iii)
Top View: (ii)
Question 4. Draw the front view, side view and top view of the given objects.

Answer:
Here are the front, side, and top views for each of the given objects.
(a) A military tent
Front View: The front of the tent is a triangle.
Side View: The side of the tent is a rectangle.
Top View: The top view of the tent is a rectangle with a line down the center representing the ridge.
(b) A table
Front View: The front view of the table shows the wider side of the tabletop and the front legs.
Side View: The side view shows the narrower side of the tabletop and the side legs.
Top View: The top view of the table is a rectangle.
(c) A nut
Front View: The front view of the hexagonal nut is a rectangle.
Side View: The side view of the hexagonal nut is also a rectangle.
Top View: The top view of the nut is a hexagon with a hexagonal hole in the center.
(d) A hexagonal block
Front View: The front view of the hexagonal block is a hexagon.
Side View: The side view of the hexagonal block is a rectangle.
Top View: The top view of the hexagonal block is also a rectangle.
(e) A dice
Front View: The front view of the dice is a square with three dots.
Side View: The side view of the dice is a square with two dots.
Top View: The top view of the dice is a square with one dot.
(f) A solid
Front View: The front view of the solid shows two cubes at the bottom and one cube on top of the left one, forming an L-shape.
Side View: The side view shows two cubes stacked vertically.
Top View: The top view shows two cubes side-by-side horizontally.
Exercise 10.2
Question 1. Look at the given map of a city.

Answer the following.
(a) Colour the map as follows: Blue-water, red-fire station, orange-library, yellow - schools, Green - park, Pink - College, Purple - Hospital, Brown - Cemetery.
(b) Mark a green ‘X’ at the intersection of Road ‘C’ and Nehru Road, Green ‘Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from Library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?
Answer:
(a) Colouring the map
The map should be coloured according to the given instructions:
- Blue: Lake, Water Plant
- Red: Fire Station
- Orange: Library
- Yellow: Primary School, Sr. Secondary School
- Green: City Park
- Pink: City College
- Purple: Hospital
- Brown: Cemetery
(b) Marking the intersections
The intersections are marked as follows:
- A green ‘X’ is marked at the intersection of Road ‘C’ and Nehru Road.
- A green ‘Y’ is marked at the intersection of Gandhi Road and Road A.
(c) Route from Library to the Bus Depot
A short street route from the Library to the Bus Depot is drawn in red. The route is as follows:
Start from the Library, move along Road A until you reach Gandhi Road. Take a right onto Gandhi Road and continue until you reach the road where the Fire Station is located. Turn right onto this road and proceed straight to the Bus Depot.
(d) Which is further east?
On a map, 'east' is to the right. The City Park is located on the right side of the map, while the Market is in the central-left area. Therefore, the City Park is further east than the Market.
(e) Which is further south?
On a map, 'south' is towards the bottom. The Primary School is located above (north of) Nehru Road, while the Sr. Secondary School is located below (south of) Nehru Road. Therefore, the Sr. Secondary School is further south than the Primary School.
Question 2. Draw a map of your class room using proper scale and symbols for different objects.
Answer:
Creating a map of your classroom is an excellent way to practice spatial representation and scaling. Here are general instructions to help you draw your own classroom map:
Instructions to Draw Your Classroom Map:
1. Measure the Dimensions:
- Use a measuring tape to find the length and width of your classroom. For example, your classroom might be 8 metres long and 6 metres wide.
2. Choose a Scale:
- A scale helps you represent large distances on a small piece of paper. A good scale might be 1 cm = 1 metre.
- Using this scale, your 8m x 6m classroom would be drawn as a rectangle of 8 cm x 6 cm on paper.
3. Draw the Outline:
- Use a ruler to draw the rectangular outline of your classroom on a sheet of paper according to the scale you've chosen.
4. Create Symbols for Objects:
- Decide on simple symbols to represent different objects in your classroom. Create a key or legend on the side of your map to explain what each symbol means.
- Examples of Symbols:
- Teacher's Desk: A larger rectangle
- Student's Desk: A smaller square or rectangle
- Door: A line with an arc showing which way it opens
- Window: A line with smaller rectangles inside
- Blackboard/Whiteboard: A thick line on one of the walls
- Cupboard: A square with a line down the middle
5. Place the Objects on the Map:
- Observe the position of objects in your classroom. Estimate their size and location.
- Draw the symbols for these objects in their correct positions on your map. For instance, show the door and windows on the correct walls. Place the teacher's desk at the front and arrange the students' desks in rows.
6. Add Labels and a Title:
- Give your map a title, such as "Map of My Classroom".
- You can add labels to important features directly on the map, like "Entrance" or "Blackboard".
- Don't forget to write down the scale you used (e.g., Scale: 1 cm = 1 m).
Question 3. Draw a map of your school compound using proper scale and symbols for various features like play ground main building, garden etc.
Answer:
Drawing a map of your school compound requires you to think about a larger area. Follow these instructions to create your own detailed map.
Instructions to Draw Your School Compound Map:
1. List Key Features:
- Walk around your school and list all the important features you want to include. Examples include: Main School Building, Playground, Garden, Library Block, Canteen, Parking Area, Assembly Ground, Basketball Court, Main Gate, etc.
2. Determine the Layout:
- Roughly sketch the positions of these features relative to each other. For example, is the playground in front of the main building or behind it? Where is the main gate?
3. Choose a Scale:
- Since a school compound is large, you'll need a different scale. For example, 1 cm = 10 metres.
- Estimate the dimensions of the school compound and the major buildings.
4. Create Symbols and a Legend:
- Design simple symbols for each feature. This makes the map easy to read.
- Example Symbols:
- Building: A large shaded rectangle
- Playground: A large open rectangle, perhaps with green shading
- Garden: An area with flower or tree symbols
- Trees: Small circles with lines
- Pathways/Roads: Double lines
- Main Gate: A break in the boundary line with two small rectangles
- Create a legend (or key) in a corner of your map to explain your symbols.
5. Draw the Map:
- Start by drawing the boundary of your school compound.
- Draw the main building first, as it is usually the central feature.
- Add other features like the playground, garden, and other buildings in their correct locations and approximate sizes according to your scale.
- Draw the pathways, roads, and the main gate.
6. Add a Title and Directions:
- Title your map, for example, "Map of [Your School's Name]".
- Add a compass rose to show the directions (North, South, East, West). This is very important for orientation.
- Include the scale you used.
Question 4. Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
Answer:
A good map to a friend's house should be simple, clear, and include landmarks. Here’s a guide on how to create one.
Instructions to Draw a Map to Your House:
1. Identify the Starting Point and End Point:
- The starting point could be a well-known place like your friend's house, the school, or a bus stop.
- The end point is your house.
2. Note Down the Route and Landmarks:
- Think about the route you would take from the starting point to your house.
- Identify important landmarks along the way. Landmarks are easily recognizable places like a post office, a big hospital, a temple/church, a grocery store, a water tank, a specific statue, or a park.
3. Create a Simple Sketch:
- You don't need a strict scale, but try to keep the distances and turns proportional.
- Draw the main roads as lines. Use thicker lines for main roads and thinner lines for smaller streets.
4. Use Clear Symbols and Labels:
- Draw simple symbols for landmarks. For example, a cross for a hospital, a rectangle with a flag for a post office, etc.
- Label the roads with their names if you know them (e.g., Mahatma Gandhi Road, Station Road).
- Clearly label your starting point, your house (end point), and all the landmarks.
5. Give Turn-by-Turn Instructions:
- Use arrows to show the direction of the route.
- Write short, simple instructions next to the map or along the route. For example:
- "Start from the Main Bus Stop."
- "Walk straight down Station Road."
- "Turn right at the City Hospital."
- "Take the second left turn."
- "My house is the third one on the right, painted blue."
6. Add a Title:
- Give your map a title, like "Map to My House".
Exercise 10.3
Question 1. Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Answer:
A polyhedron is a three-dimensional solid figure whose surfaces are flat polygons. For a closed solid shape to be formed, it must have at least 4 faces.
(i) 3 triangles?
No, a polyhedron cannot have 3 triangles as its faces. A polyhedron is a closed 3D shape. With only 3 triangles, you can form an open shape, but you cannot close it to form a solid. The minimum number of faces required to form a polyhedron is 4.
(ii) 4 triangles?
Yes, a polyhedron can have 4 triangles as its faces. This specific polyhedron is called a triangular pyramid (also known as a tetrahedron). It has a triangular base and three other triangular faces that meet at a common vertex.
(iii) a square and four triangles?
Yes, a polyhedron can be formed with a square and four triangles. This shape is a square pyramid. It has a square base and four triangular faces that meet at a single vertex (apex) above the base.
Question 2. Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
Answer:
To answer this question, we need to consider the minimum number of faces a polyhedron can have and whether we can construct a polyhedron for any number of faces greater than that minimum.
Analysis:
A polyhedron is a closed three-dimensional figure with flat polygonal faces. The simplest possible polyhedron is a pyramid.
Let's consider a pyramid with a base that is an n-sided polygon (an n-gon).
- The base itself is one face.
- From each of the n sides of the base, a triangular face rises to meet at a common apex. This gives us n triangular faces.
Therefore, the total number of faces for a pyramid with an n-sided base is $n + 1$.
The simplest polygon for a base is a triangle (where $n=3$).
- If the base is a triangle ($n=3$), the total number of faces is $3 + 1 = 4$. This is a triangular pyramid.
- If the base is a square ($n=4$), the total number of faces is $4 + 1 = 5$. This is a square pyramid.
- If the base is a pentagon ($n=5$), the total number of faces is $5 + 1 = 6$. This is a pentagonal pyramid.
- ...and so on.
We can construct a pyramid with a base of any number of sides $n \geq 3$. This means we can create polyhedrons with $4, 5, 6, 7, ...$ faces.
The minimum number of faces a polygon (the base) can have is 3. Thus, the minimum number of faces a polyhedron (a pyramid in this case) can have is $3+1 = 4$.
Conclusion:
Yes, it is possible to have a polyhedron with any given number of faces, provided the number of faces is 4 or more.
A polyhedron cannot be formed with fewer than 4 faces as it is impossible to create a closed 3D space with only 1, 2, or 3 flat faces.
Question 3. Which are prisms among the following?
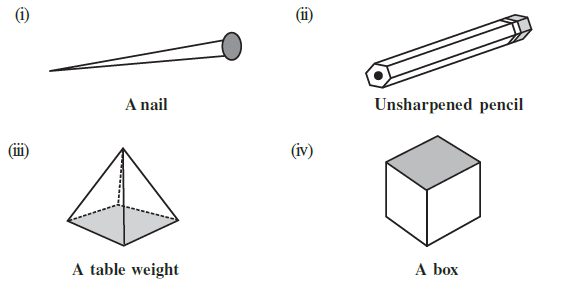
Answer:
A prism is a type of polyhedron that has two identical and parallel polygonal bases, and whose other faces (lateral faces) are parallelograms, formed by connecting the corresponding vertices of the two bases.
Let's analyze each object to see if it fits the definition of a prism:
(i) A nail
A nail has a circular head and a pointed body (cone). It does not have polygonal bases. Therefore, a nail is not a prism. It is also not a polyhedron because it has a curved surface.
(ii) Unsharpened pencil
An unsharpened pencil has a hexagonal cross-section. This means it has two identical and parallel hexagonal bases (at the top and bottom). The faces connecting these bases are rectangles (which are a type of parallelogram). Therefore, an unsharpened pencil is a prism (specifically, a hexagonal prism).
(iii) A table weight
The table weight shown is a square pyramid. It has one square base, but its other faces are triangles that meet at a single point (apex). It does not have two identical, parallel bases. Therefore, a table weight is not a prism.
(iv) A box
A box (specifically, a cuboid or a cube) has two identical and parallel square or rectangular bases. The other four faces are also rectangles. This perfectly fits the definition of a prism. Therefore, a box is a prism (a rectangular prism or a square prism).
Conclusion:
The prisms among the given objects are:
- (ii) Unsharpened pencil
- (iv) A box
Question 4.
(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Answer:
(i) How are prisms and cylinders alike?
Prisms and cylinders share a fundamental structural similarity:
- Both prisms and cylinders have two bases that are identical (congruent) and parallel to each other.
- The main difference is the shape of the base. A prism has a polygon as its base, while a cylinder has a circle as its base.
- One can think of a cylinder as a special type of prism where the base polygon has an infinite number of sides, which makes it a circle. If you take a prism with a base that is a regular polygon (e.g., a pentagon, hexagon, etc.) and keep increasing the number of sides of the base, the prism will look more and more like a cylinder.
(ii) How are pyramids and cones alike?
Pyramids and cones also have a key structural similarity:
- Both pyramids and cones have a single base and a single vertex (called an apex) that is not in the plane of the base.
- The lateral surfaces of both shapes are formed by connecting every point on the boundary of the base to the apex.
- The main difference is the shape of the base. A pyramid has a polygon as its base (leading to triangular lateral faces), while a cone has a circular base (leading to a curved lateral surface).
- Similar to the relationship between prisms and cylinders, a cone can be thought of as a special type of pyramid. If you take a pyramid with a regular polygonal base and increase the number of sides indefinitely, it will become a cone.
Question 5. Is a square prism same as a cube? Explain.
Answer:
No, a square prism is not always the same as a cube, but a cube is a special type of square prism. Here is the explanation:
Definition of a Square Prism:
A square prism is a prism that has two identical and parallel square bases. Its other four faces (the lateral faces) are rectangles. The height of the prism is the perpendicular distance between the two square bases.
Definition of a Cube:
A cube is a special type of polyhedron where all six faces are identical squares. This means that its length, width, and height are all equal.
Explanation of the Relationship:
A square prism has a square base, let's say with side length 's'. The lateral faces are rectangles. The height of these rectangles (which is the height of the prism) can be any value 'h'.
- If the height 'h' of the square prism is not equal to the side length 's' of its square base, then the lateral faces are rectangles, not squares. This shape is a cuboid (a rectangular prism), but not a cube.
- If the height 'h' of the square prism is equal to the side length 's' of its square base ($h = s$), then the rectangular lateral faces also become squares. In this specific case, all six faces of the prism are identical squares, which is the definition of a cube.
Therefore, a cube is a special case of a square prism where the height is equal to the side length of the base. An object like a shoebox can be a square prism, but it is not a cube. An object like a standard die is a cube, and it is also a square prism.
Question 6. Verify Euler’s formula for these solids.

Answer:
Euler's formula for polyhedrons states a relationship between the number of Faces (F), Vertices (V), and Edges (E) of any convex polyhedron. The formula is:
F + V - E = 2
We need to count the number of faces, vertices, and edges for each of the given solids and verify if they satisfy this formula.
For Solid (i)
This solid is a frustum of a pentagonal pyramid.
1. Counting the Faces (F):
- There is one pentagonal face at the top.
- There is one pentagonal face at the bottom.
- There are 5 trapezoidal faces on the sides.
Total number of Faces, F = 1 (top) + 1 (bottom) + 5 (sides) = 7.
2. Counting the Vertices (V):
- There are 5 vertices on the top pentagonal face.
- There are 5 vertices on the bottom pentagonal face.
Total number of Vertices, V = 5 (top) + 5 (bottom) = 10.
3. Counting the Edges (E):
- There are 5 edges on the top pentagonal face.
- There are 5 edges on the bottom pentagonal face.
- There are 5 vertical edges connecting the top and bottom faces.
Total number of Edges, E = 5 (top) + 5 (bottom) + 5 (sides) = 15.
4. Verifying Euler's Formula:
We plug the values into the formula F + V - E = 2.
$F + V - E = 7 + 10 - 15$
$= 17 - 15$
$= 2$
Since the result is 2, Euler's formula is verified for Solid (i).
For Solid (ii)
This solid is a square prism (or cube) with a square pyramid on top.
1. Counting the Faces (F):
- There is one square face at the bottom.
- There are 4 rectangular faces on the sides of the prism part.
- There are 4 triangular faces on the top pyramid part.
Total number of Faces, F = 1 (bottom) + 4 (sides) + 4 (top) = 9.
2. Counting the Vertices (V):
- There are 4 vertices on the bottom square base.
- There are 4 vertices where the prism and pyramid meet.
- There is 1 vertex at the apex of the pyramid.
Total number of Vertices, V = 4 (bottom) + 4 (middle) + 1 (top) = 9.
3. Counting the Edges (E):
- There are 4 edges on the bottom square base.
- There are 4 vertical edges of the prism part.
- There are 4 edges around the square where the prism and pyramid meet.
- There are 4 edges going from the middle square to the apex.
Total number of Edges, E = 4 (bottom) + 4 (vertical) + 4 (middle) + 4 (top) = 16.
4. Verifying Euler's Formula:
We plug the values into the formula F + V - E = 2.
$F + V - E = 9 + 9 - 16$
$= 18 - 16$
$= 2$
Since the result is 2, Euler's formula is verified for Solid (ii).
Question 7. Using Euler’s formula find the unknown.
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
Answer:
We will use Euler's formula for polyhedrons, which is F + V - E = 2, to find the unknown value in each column of the table.
Column 1:
Given:
- Faces (F) = ?
- Vertices (V) = 6
- Edges (E) = 12
Using the formula:
$F + V - E = 2$
$F + 6 - 12 = 2$
$F - 6 = 2$
$F = 2 + 6$
$F = 8$
The number of faces is 8.
Column 2:
Given:
- Faces (F) = 5
- Vertices (V) = ?
- Edges (E) = 9
Using the formula:
$F + V - E = 2$
$5 + V - 9 = 2$
$V - 4 = 2$
$V = 2 + 4$
$V = 6$
The number of vertices is 6.
Column 3:
Given:
- Faces (F) = 20
- Vertices (V) = 12
- Edges (E) = ?
Using the formula:
$F + V - E = 2$
$20 + 12 - E = 2$
$32 - E = 2$
$E = 32 - 2$
$E = 30$
The number of edges is 30.
The completed table is:
| Faces | 8 | 5 | 20 |
| Vertices | 6 | 6 | 12 |
| Edges | 12 | 9 | 30 |
Question 8. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Answer:
To determine if a polyhedron can have a given number of faces, edges, and vertices, we must check if these numbers satisfy Euler's formula for polyhedrons.
Given values:
- Number of Faces (F) = 10
- Number of Edges (E) = 20
- Number of Vertices (V) = 15
Euler's Formula:
$F + V - E = 2$
Now, we substitute the given values into the Left Hand Side (L.H.S.) of the formula and see if it equals the Right Hand Side (R.H.S.), which is 2.
L.H.S. = $F + V - E$
L.H.S. = $10 + 15 - 20$
L.H.S. = $25 - 20$
L.H.S. = $5$
Comparing the result with Euler's formula:
We found that $F + V - E = 5$.
However, for any valid polyhedron, Euler's formula states that $F + V - E$ must equal 2.
Since $5 \neq 2$, the given numbers do not satisfy Euler's formula.
Conclusion:
No, a polyhedron cannot have 10 faces, 20 edges, and 15 vertices because these values do not satisfy Euler's formula.

